Selected Articles from the
August 2001 Odyssey

Editor: Terry Hancock

• The LaGrange Points and You, Terry Hancock
• The Surf Report, Diane Rhodes

The LaGrange Points and You

Terry Hancock

They're called the ``LaGrange Points'' after the scientist who first described them, or the ``Libration Points'' after the way a spacecraft will oscillate or librate at the points, retaining the same average position relative to the two large bodies they orbit with, and they are individually known by number as the ``L1'' to ``L5'' points, the last of them lending its name to one of the principal space enthusiast organizations of the last century. But do you know what, where, and why they actually are?

Unfortunately, the mathematical basis of the LaGrange points involves fairly difficult orbital mechanics and requires an understanding of vector differential equations. Indeed, multi-body orbital mechanics has been one of the main reasons for developing that mathematics, and it continues to push methods of analysis even today.

Mathematicians like to propose examples of practical applications for their work and especially love being able to claim that some result or other could be arrived at by no other means. This has had the unfortunate consequence that the LaGrange points are generally presented with no intuitive explanation at all, as if they just bubbled up out of the mathematical soup of differential equations in some completely ineffable way!

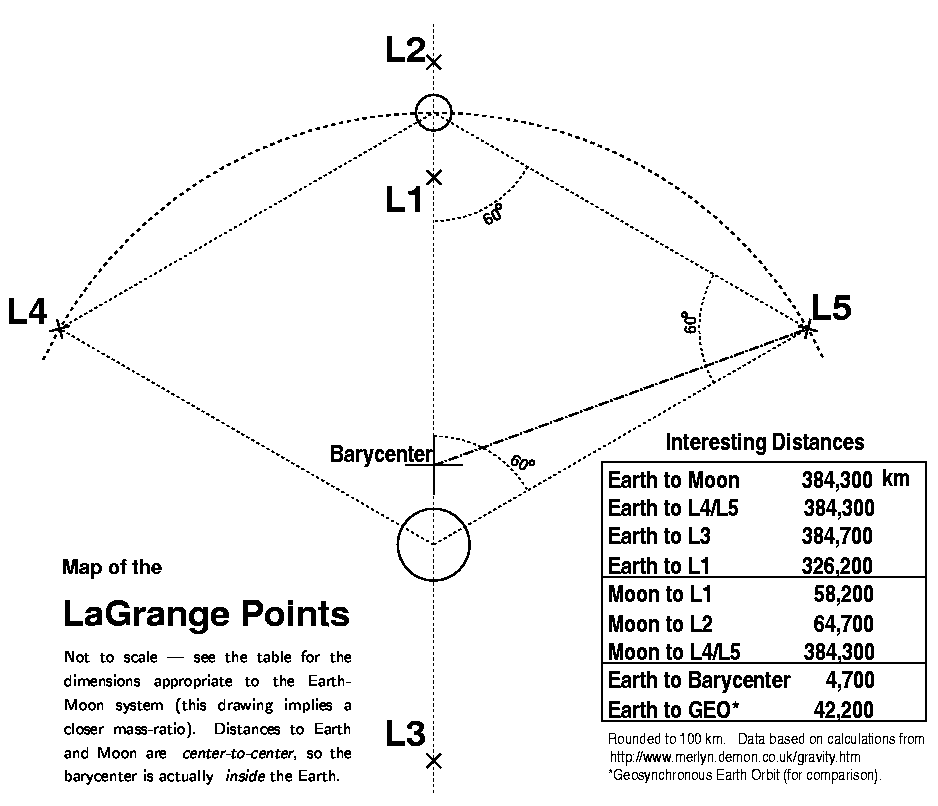Map of LaGrange Points. Click to enlarge.

However, while it's probably true that no one would have thought up the LaGrange points without extensive mathematical analysis, it is possible to make an intuitive argument for the sensibility of the results, and I find that this greatly improves my ability both to remember and to predict their properties and positions.

Where are they?

For the record, the LaGrange points exist only in a system where there are two large orbiting bodies, which are otherwise relatively undisturbed by outside forces. This is true of the Earth-Moon system, of moons of the giant planets, and of each of the planets themselves, where the Sun is the other body. It may seem strange that the other planets do not interfere, but this is for the same reason that the planets' orbits can themselves each be thought of as ordinary two-body orbits (if they weren't, they wouldn't follow Keplerian motion, and orbital mechanics would've taken us a lot longer to figure out!). Because it's confusing otherwise, I'll refer to the ``larger body'' as the Earth and the ``smaller body'' as the Moon, but you should understand that the rules apply to other systems as well.

Furthermore, the LaGrange points remain stationary relative to the line between the Earth and Moon - which of course means that they are orbiting with the same period (i.e. one month). Also, the LaGrange points only work for objects that are much, much smaller than the planets, like spaceships or space stations - they don't work for other planets, though a small asteroid might be captured in one.

Points 1, 2, and 3 lie along the Earth-Moon axis. L1 is in-between, L2 is on the outside of the Moon, and L3 is on the outside of the Earth. Thus, L1 lies most of the way to the moon, but in-between the Earth and Moon, while L2 hovers over the far-side of the Moon, and L3 is on the opposite side from the Moon from the Earth, and slightly further from the Earth than the Moon is (but closer to the center of gravity, or barycenter, see the table on page 3).

Points 4 and 5, on the other hand, lie close to the Moon's orbital track about the Earth - at the point of an equilateral triangle, one side of which is the line connecting the Earth and Moon (not the barycenter and the Moon). This means that the points are 60^° behind (L4) and ahead (L5) of the Moon in its orbit.

For the Earth-Moon system, the ratio between the mass of the Moon and Earth is about 1:81 and for such large mass ratios, the L4 and L5 points are stable in a useful sense that we will come to below.

L1 Point

The easiest of the points to understand, and perhaps the only one that most people would have thought of intuitively, would be the L1 point, which lies on the line between the two bodies. It's pretty obvious that somewhere along this line, there's a point where the gravitational pull of the Earth is exactly canceled by the pull of the Moon. Indeed, Jules Verne mentioned this in his First Men in the Moon, although he erroneously predicted that this would be the only part of the journey where you would experience zero gravity conditions.

This point is not quite the L1 point, for one simple reason - the system is rotating! Because of that, the familiar relationship of gravity and ``centrifugal force'' applies. Or in more accurate terms, the object would keep going in a straight line if there weren't some residual gravity to pull it into a circular orbit. That means that the L1 point is a little closer to the Earth than the point where the gravities balance.

From an engineering perspective, this point serves much the same applications for the Moon that geosynchronous orbit does for the Earth - objects in this position will hover in the same position in the sky as viewed from the Moon's surface. This depends on the additional fact that the Moon is tidally locked, meaning that it has the same orbital and rotational periods or that it always turns the same face towards the Earth.

Clearly, this point is not stable, however: If you were one inch closer to the Moon than the Earth, the Moon's pull would be slightly stronger. So you'd be pulled out of position even further to a point where the pull would be stronger still, and so on. This will not pull you straight to the Moon because of coriolis effects - eventually you would be pulled into a general three-body orbit around the Earth and Moon which is quite unstable, leading to one of three eventualities: a stable, lower orbit around one of the two worlds, ejection from the system entirely, or impact into one of the two.

L2 and L3 Points

These points also lie along the Earth-Moon axis, but they lie on the ``outside''. L2 is over the far side of the Moon. This is less intuitive, but we can still come to a useful understanding of it, by considering equivalent two-body orbits.

Consider this, we describe orbits about planets as though all the mass in the planet were concentrated in its center. This is a special property of spheres - that from any angle, the off-axis forces from the sphere's mass exactly cancel, so that it's just as if all the mass were concentrated at a single point. This is why, for example, orbits don't care how large the body being orbited is - just how massive (i.e. heavy) it is.

For a mass distributed into two spherical bodies, this property is true in only two places: along the line connecting the two masses. From that perspective, the center of gravity of both spheres lies in exactly the same direction, and therefore the gravity of both exactly adds up. As long as you remain on this line, you can think of the two masses as being added together and lying at the center of gravity of the whole system. Therefore, for the instant you cross this line, the physics of the orbit is exactly like a two-body orbit.

There is one particular orbit for which this is not an instantaneous effect, and that's the particular orbit which is synchronous with the orbit of the two larger bodies. In that orbit, your orbital velocity is exactly enough to keep you on the centerline. Thus the two bodies ``feel'' like one body at the center of mass, and your orbit is just like a two-body orbit.

This is true for both the L2 and L3 orbits. The gravitational force is not equivalent to the sum of the larger mass bodies, since you are much closer to one than the other, but the result is definitely equivalent to a simple orbit around a body of a certain mass lying at the center of mass of the system.

Since adding the Moon's mass to the Earth's makes little difference, it should come as no surprise that the L2 and L3 points are quite near the Moon's orbit - L3 is 180^° away in a relatively isolated piece of space, while L2 has an excellent vantage point over the far side of the Moon.

Like L1, these points are not stable. If you are just a bit away from them, you will be pulled (gently) away from them, with a force that will gradually get stronger until you are pulled completely away into an unstable three-body orbit. The forces required to combat this pull are small, however, and a spacecraft can stay in this position with a very small expenditure of reaction mass for stationkeeping.

The L2 point can serve the same ``synchronous orbit'' purpose for the far side of the Moon that the L1 point provides for the near side. The L3 point, though, has little engineering value in the Earth-Moon system, its main distinction being that it never sees the Moon.

L4 and L5 Points

The last points are a bit harder to understand, though they have a geometrical elegance that definitely draws one's attention to them. They lie at exactly the same distance from the two bodies as the two bodies lie from each other, so that the three together form the points of an equilateral triangle.

Why is this stable, though?

Let's start with the case where the two larger bodies are the same mass. In this case, the L4 and L5 points lie at a right angle to the line between the larger bodies, orbiting the center of mass. From this position, the lateral pull of the two planets' gravities exactly cancel so there's nothing pulling the object along its orbit. All the force is directed towards the center of mass instead.

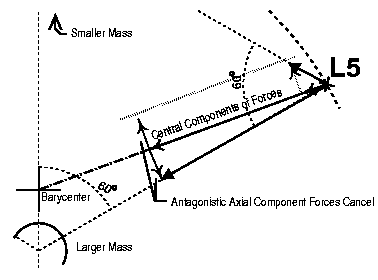Forces acting on a body at the L4 or L5 point -- the antagonistic forces of Earth and Moon are positioned so that the residual force points at the the center of mass.

Just as with the L2 and L3 points, this balance is only maintained so long as the body stays in its relative location to the large planets. This requires the orbit to be synchronous, which limits us once again to a particular point.

Now what happens when the mass of one of the planets is larger than the other?

The center of mass of the whole system is closer to the larger body then. But the lateral perturbing force of the larger body is larger than the perturbing force from the smaller body. Thus the smaller body must be pulling more directly along the orbit to compensate. These two effects cancel out exactly, and so the equilateral triangle relationship is preserved, although the center of mass is placed differently (see the preceding figure).

Although the L4 and L5 points are also synchronous to the surface of the Moon, they are so much further away than the L1 and L2 points that they are of less use as communications points (except that they see both near and far sides of the moon so they can fill out the coverage). Unlike the other three points, however they are stable. Any error in position results not in an unstable orbit, but in a stable ``libration orbit'' around the actual point (that is, it will slowly circle the point once a month). This is true over a fairly large patch of space. Thus space stations parked near the L4 or L5 points will stay put with no expenditure of stationkeeping reaction mass. Furthermore, more than one station can populate the point.

There's no particular reason to prefer the L5 point over the L4 point. The L5 point leads, while the L4 point trails - thus the L4 point is shielded somewhat being in the Moon's ``meteoroid shadow'' after a fashion. On the other hand, debris originating at the moon may be more likely to find its way to the L4 point than the L5. These are theoretical concerns of little import however, and we now know by direct measurement (from the Japanese Hiten probe) that these points are quite empty, the dust not being significantly thicker there than anywhere else in the Earth-Moon system.

File translated from T_EX by T_TH, version 2.25.
On 18 Jan 2002, 12:53.

Copyright © 1998-2003 Organization for the Advancement of Space Industrialization and Settlement. All Rights Reserved.